* 본 내용은 딥러닝을 공부하며 정리한 내용들입니다. 혹여나 잘못 서술되어있는 지식들은 바로잡아주시면 감사하겠습니다.
DL (Deep Learning), 딥 러닝을 구글에 검색했을 때 보이는 정의들은 다음과 같다.
쉽게 이야기하면 다음과 같이 이야기할 수 있고,
인간의 두뇌에서 영감을 얻은 방식으로 데이터를 처리하도록 컴퓨터를 가르치는 인공 지능(AI) 방식
어렵게 정의하면 다음과 같이 정의할 수 있을 것이다.
'비선형 변환기법'의 조합을 통해 높은 수준의 추상화(abstractions, 다량의 데이터나 복잡한 자료들 속에서 핵심적인 내용 또는 기능을 요약하는 작업)를 시도하는 기계 학습 알고리즘의 집합
내가 딥러닝을 공부하면서 가장 보편적으로 많이 봤던 정의는 다음과 같았다.
머신 러닝(Machine Learning)의 특정한 한 분야로서 인공 신경망(Artificial Neural Network)의 층을 연속적으로 깊게 쌓아올려 데이터를 학습하는 방식
조금 더 이해하기 쉬운 그림들을 가지고 와봤다.

그렇다면 딥러닝에서 학습을 한다는 의미는 무엇일까?
크게 보면 데이터를 가장 잘 설명하는 ((f(x)))를 찾는 과정이라고 생각하면 된다.

데이터를 학습하기 위해서는 학습 모델 구축을 위한 train data와 구축한 모델을 테스트 하기 위한 test data로 분리해줘야하는데,
상황에 따라 train data, validation data, test data로 나누기도 한다.
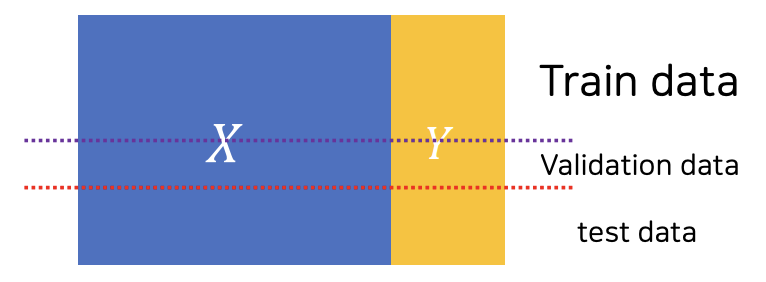
이때, 학습을 하는 목적은 손실 함수를 최소화하는 것에 있다.
조금 더 수학적으로 이를 표현하자면,
((X_{tr}, X_{te}))는 각각 train, test data 값의 ((x))값이고, ((Y_{tr}, Y_{te}))는 각각 train, test data 값의 ((y))값이라고 하자.
구축한 모델 ((f))로부터 예측된 결과는 각각 ((\hat{Y_{tr}}, \hat{Y_{te}}))로 표시한다고 하자.
이때 ((L(Y_{te}, \hat{Y_{te}})))는 테스트한 결과의 손실이며, ((L(Y_{te}, \hat{Y_{te}})))는 주기적으로 테스트를 하며 최소화를 한다.
즉, 알고리즘이 예측한 값과 실제 정답의 차이를 비교한 값들이 최소화가 되어야 잘못 예측하는 정도가 줄어들었다고 할 수 있기에,
우리는 학습을 통해 이를 최소화하는 것을 목적으로 한다는 것이다.
또한, ((L(Y_{te}, \hat{Y_{te}})))를 최소화하는 파라미터 ((\Theta ))를 찾는 과정이라고 할 수 있는데, 이는 나중에 자세하게 다루겠다.
-
데이터 학습을 위해서 train 데이터와 test 데이터로 나눈다고 언급했는데, 이를 나누는 이유는 다음과 같다.
train 과정에서 학습을 했다고 해서 정답만을 말할 수 있는 것이 아니기 때문에 모델이 나온 후,
최종적으로 모델이 '한 번도 보지 못한' 데이터에 대해 평가를 해야 실제로도 작동을 잘할 수 있는지 판단할 수 있다.
이 과정에서 test 데이터를 활용하기 때문에, 데이터를 나눠야하는 것이다.
즉, test 데이터는 모델을 평가하는 용도로 사용하는 것이다.
일반적으로 이 둘로 분류를 할 때는 8:2의 비율이 되도록 분리한다.
하지만, 분류 문제에서 학습 데이터에 특정 라벨이 더 많이 포함되는 경우가 생길 수 있다.
이에 따라 학습 데이터에서 특정 라벨만 학습이 되어 '과적합'의 문제가 발생 할 수 있다는 것이다.
이를 해결하기 위해 우리는 '교차 검증 (Cross Validation)'을 사용할 수 있다.
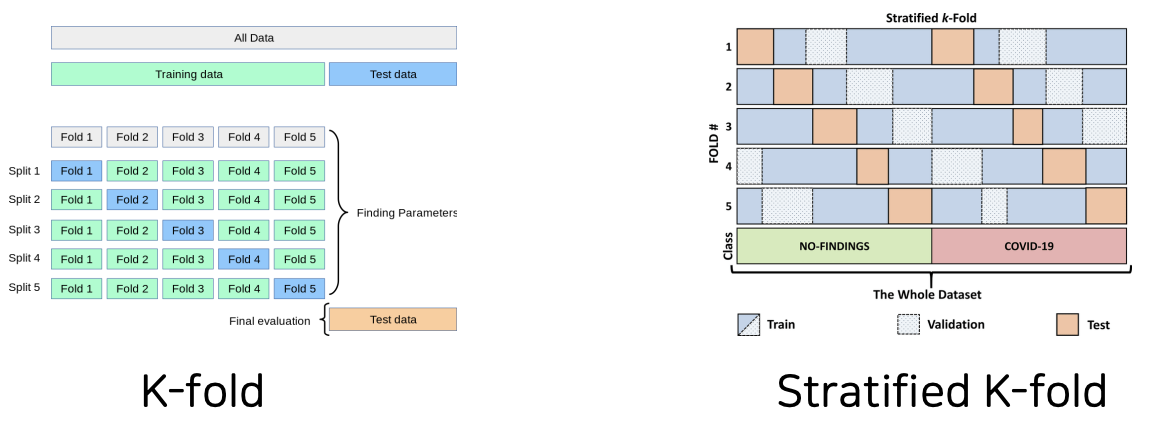
교차 검증에는 크게 K-fold 교차 검증와 Stratified K-Fold 교차 검증이 있는데,
- K-Fold : 데이터를 k개의 그룹으로 나눈 후 각 그룹을 각각 테스트 데이터로 하여 학습
- Stratified K-Fold : K-Fold과 큰 틀에서 같지만 각 그룹마다 전체 라벨의 비율을 유지한다는 점에서 차이 있음
그림으로 표현하면 다음과 같다.
-
학습 단계의 방식으로는 순전파(forward propagation)과 역전파(backward propagation)로 나눌 수 있다.
순전파(forward propagation) - 정방향 계산
- 𝜃를 이용하여 연산을 진행하는 부분으로, 연산 결과와 실제 값의 차이인 ((L(Y_{te}, \hat{Y_{te}})))를 비교함
- 𝐿𝑜𝑠𝑠 𝑓𝑢𝑛𝑐𝑡𝑖𝑜𝑛으로는 회귀의 경우에는 MAE, MSE, RMSE를 주로 사용하고, 분류의 경우에는 cross-entropy 사용
역전파(backward propagation) - 역방향
- 순전파의 연산 결과로부터 Loss function을 최소화하는 과정
- “Chain Rule”이라는 것을 이용하여 𝜃를 업데이트하는 과정을 반복적으로 수행
- 미분을 하는 방식은 시간이 매우 오래걸리기 때문에 “Gradient Descent” 방식을 많이 이용함
여기서 언급된 내용들은 뒤에 포스팅 될 내용에서 더 자세히 설명하겠다. 지금은 개괄적인 설명이므로 이렇다. 정도의 개념만 가져가자.
1. 초기에 가중치를 임의로 설정한 후 연산 진행 (순전파)
2. 1 의 결과를 토대로 손실 함수를 이용하여 예측값과 실제값의 차이를 확인함
2-1. 해당 부분에서 손실함수로 MSE, RMSE를 사용할 수 있음
2-2. 분류 문제의 경우에는 Cross-entropy loss를 고려함
3. Gradient Descent 기법을 통해 파라미터 𝜃를 업데이트
하고 난 후 1 ~ 3과정을 무한 반복하면 된다.
-
옵티마이저(Optimizer)
: 손실 함수로 얻은 오차를 이용해 역전파로 가중치를 업데이트하는 방법
- 역전파 과정에서 학습속도를 빠르고 안정적으로 하는 것을 목표로 함
- Gradient Descent를 조금 더 효율적으로 할 수 있는 방법론을 제시함
-
전반적인 딥러닝의 학습 과정을 도식화하면 다음과 같다.


댓글